本文为了理清贝叶斯网络, 信念传播以及因子图之间的关系。

对于inference problems,信念传播(BP)是一种重要的解决方法
条件概率
条件概率就是求在B发生的概率下A发生的概率\(P(A|B)\) 。 \[ P(A|B) = \frac{P(A \cap B)}{P(B)} \]
边缘独立与条件独立
如果两个事件独立,那么满足如下等式: \[ P(A \cap B) = P(A)P(B) \]
贝叶斯网络介绍
一个贝叶斯网络是一个__有向无环图(DAG)__,也叫信念网络(belief network)。
贝叶斯网络常常用作是医疗诊断,语言识别等专家系统。
链式规则
对于一两个随机变量\(X\), \(Y\),为了找到他们的联合分布,我们可以定义如下条件概率: \[ P(X,Y)=P(X|Y)\cdot P(Y) \] 如果有多个随机变量\(X_1...X_n\)的话: \[ P(X_n,...,X_1) = P(Xn|X_{n-1},...,X_1)\cdot P(X_{n-1},....,X_1) \] 其中可以继续拆分,如(n=4):
\[ P(X_4, X_3, X_2, X_1) = P(X_4|X_3,X_2,X_1)\cdot P(X_3, X_2, X_1) = P(X_4|X_3,X_2,X_1)\cdot P(X_3|X_2,X_1)\cdot P(X_2, X_1) =... \]
通过公式进行抽象就是过程:
\[ P \Bigg( \bigcap_{k=1}^nX_k \Bigg) = \prod_{k=1}^nP\Bigg(X_k\Bigg| \bigcap_{j=1}^{k=1}X_j \Bigg) \]
贝叶斯网络
比如下图贝叶斯网络:
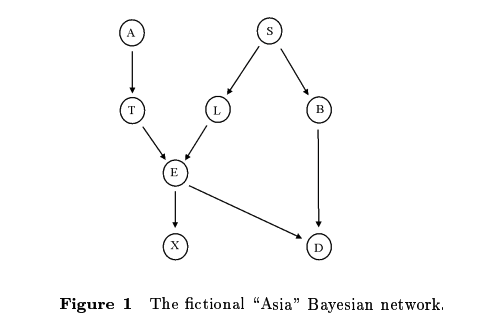
给定一个关键词"Asia"
参考
https://longaspire.github.io/blog/%E5%9B%A0%E5%AD%90%E5%9B%BE%E4%BB%8B%E7%BB%8D/